Máquinas de Soporte Vectorial para clasificación de patrones con kernels basados en polinomios ortogonales
Luis Padierna (Universidad de Guanajuato)
Friday, November 8th. 15.00 h GMT
Abstract:
Las máquinas de soporte vectorial son un modelo de aprendizaje automático, capaz de resolver problemas de clasificación, regresión, detección de valores atípicos, agrupamiento, entre otros. Entre sus diferencias principales con otros modelos destacan su sólida formulación teórica, la capacidad de cuantificar un valor esperado en generalización y el uso de funciones kernel como estrategia para tratar problemas no linealmente separables. Diversos kernel han sido desarrollados para su uso con MSV, tales como los kernels no paramétricos, el kernel Wavelet, y kernels basados en polinomios ortogonales (Hermite, Laguerre, Gegenbauer,…). En esta plática se revisará el estado del arte sobre MSV con kernels ortogonales, se discutirán resultados experimentales interesantes con estos kernels al ser comparados con kernels clásicos como el RBF y lineal. Finalmente, se mostrarán ejemplos de su uso con códigos de Python y se discutirán los problemas abiertos en esta línea de investigación.
Generalized Charlier polynomials: regularisation and composition of birational transformations
Cristina Rodríguez-Perales (Universidad de Almería)
Friday, October 4th. 14.00 h GMT
Abstract:
In this work we study connection between the recurrence coefficients of generalized Char-
lier polynomials and the third and fifth Painlev´e equations. With that purpose we tackle the
regularisation of a differential system satisfied by the recurrence coefficients of these polynomi-
als. Furthermore, we show how iterated regularisation allows us to obtain decompositions of
birational transformations into simple ones.
This talk is based on a joint work with Dr. Galina Filipuk (University of Warsaw, Poland).
Polinomios ortogonales de Zernike tipo Sobolev. Cuadratura e interpolación
Gabriel Arturo Pulido (Universidad Nacional de Colombia)
Friday, September 6th. 14.00 h GMT
Abstract:
Presentamos una familia de polinomios ortogonales clásicos sobre la bola unidad, centrándonos en los polinomios ortogonales de Zernike. Discutimos algunas aplicaciones en sistemas ópticos y varios productos internos de Zernike tipo Sobolev. Mostramos varios ejemplos y presentamos un tipo especial de cuadratura e interpolación encontrados en la literatura reciente para funciones definidas en el disco unitario, utilizando polinomios de Zernike, donde uno de los principales resultados es el siguiente.
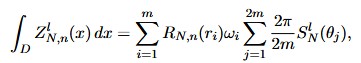
es la familia de polinomios de Zernike de grado N+2n, 
es un polinomio radial, y 
es una función angular.
Finalmente, presentamos una representación análoga con la familia de Sobolev de Zernike y la representación de Zernike en dimensiones superiores.
Matrix functions approximation using matrix coherent pairs
Edinson Fuentes (Universidad de los Llanos)
Friday, May 31st. 14.00 h GMT
Abstract:
In this talk, the concept of matrix coherent pair for two regular matrix linear functionals is presented [E. Fuentes and L. E. Garza. Coherent pairs and Sobolev-type orthogonal polynomials on the real line: an extension to the matrix case. J. Math. Anal. Appl. 518 (2023), no. 1, Paper No. 126674, 21 pp.]. This coherence relation allows to compute Sobolev-type matrix orthogonal polynomials and Fourier-Sobolev matrix-value coefficients efficiently.
The structure of the talk is the following. In the first part, some basic properties of both Laguerre and Laguerre-Sobolev matrix polynomials are presented. Laguerre matrix polynomials were introduced by Jódar in [Jódar, L.; Company, R.; Navarro, E., Laguerre matrix polynomials and systems of second-order differential equations. Appl. Numer. Math. 15 (1994), no.1, 53–63.], and these examples motivate the study of coherent pairs and Sobolev-type polynomials in the matrix case. In the second part, algorithms to compute both matrix coherent pairs and Sobolev-type matrix polynomials are state and these are used in the matrix functions approximation. Finally, the results are illustrated with a numerical example.
Polinomios ortogonales de Sobolev para resolver la ecuación de Schrödinger estacionaria
Teresa E. Pérez (Universidad de Granada)
Friday, April 24th. 14.00 h GMT
Abstract:
En la formulación variacional del problema de valores en la frontera del oscilador armónico, aparecen de forma natural productos escalares de Sobolev. En esta charla estudiamos las sucesiones de polinomios ortogonales de Sobolev asociados a este producto escalar y sus representaciones en términos de los polinomios de Gegenbauer, y mostramos un algoritmo para generar estos polinomios de forma recursiva.
También obtenemos la asintótica relativa exterior entre estos polinomios de Sobolev y los polinomios clásicos de Legendre. Además analizamos la funciones test del problema en términos de familias de polinomios de Sobolev, y daremos la solución del problema en términos de sumas de Fourier-Sobolev. Finalmente, mostraremos un ejemplo numérico de método espectral definido.
Este es un trabajo conjunto con L. Fernández, F. Marcellán y M. A. Piñar.
s-Riesz minimum energy problems with external fields
Ramón Orive (Universidad de la Laguna)
Friday, March 22nd. 15.00 h GMT
Abstract:
In this talk, minimum energy problems (a.k.a. equilibrium problems) for s-Riesz potentials (s>0) with external fields are considered in R^d, d\geq 1. Our main concern is the existence of the minimizing (equilibrium) measure and the possible compactness of its support. In addition to providing necessary and/or sufficient conditions in these senses, we focus on some particular examples.
The interest of the speaker in this topic comes from the important applications of the logarithmic potentials (s=0) to study the asymptotic behavior of orthogonal polynomials, which will be briefly reminded.
This talk is based on joint works with P. Dragnev (PFW, IN, USA), E. B. Saff (Vanderbilt Univ., TN, USA) and F. Wielonsky (Univ. Aix–Marseille, France).
Recent advances on multiple orthogonal polynomials
Manuel Mañas (Universidad Complutense de Madrid)
Friday, February 23th. 15.00 h GMT
Abstract:
In this talk we will review our latest research on multiple orthogonality. We will discuss the Favard spectral theorem for bounded band matrices admitting a positive bidiagonal factorization, and mixed multiple orthogonal polynomials.
Additionally, we will comment on the recent discovery of hypergeometric expressions for multiple orthogonal polynomials of Hahn and all their descendants in the multiple Askey scheme.
Symmetrization process and its application to a family of truncated orthogonal polynomials
Juan C. García-Ardila (Universidad Politécnica de Madrid)
Friday, November 24th. 15.00 h GMT
Abstract:
In this talk, we introduce the truncated Laguerre polynomials $P_n(x,z)$, orthogonal with respect to the linear functional
$$\prodint{\elln,p}=\int_{0}^zp(x)x^\alpha e^{-x}dx,\qquad\alpha>-1$$
and their connection with the polynomials $S_n(x,z)$ obtained through the symmetrization process. As a consequence, several properties of the polynomials $P_n(x,z)$ and $S_n(x,z)$ are presented. In particular, taking into account the relation between the parameters of the three-term recurrence relations that they satisfy, we get results about discrete Painlevé and Painlevé equations, electrostatic interpretation of the zeros of such polynomials as well as the dynamics of the zeros in terms of the parameter $z$. Finally, Gaussian quadrature rules are discussed.
La cadena de nacimiento y muerte generada por los polinomios de Jacobi asociados
Claudia Juárez (Universidad Nacional Autónoma de México, UNAM)
Friday, October 27th. 14.00 h GMT
Abstract:
En esta charla, veremos una interpretación probabilística de los polinomios de Jacobi asociados. Estos polinomios se pueden construir a partir de la relación de recurrencia de tres términos de los polinomios de Jacobi clásicos mediante un desplazamiento del índice entero 𝑛 por un número real 𝑡. Bajo ciertas condiciones, este proceso da como resultado una matriz estocástica tridiagonal doblemente infinita, que puede interpretarse como la matriz de probabilidades de transición de una cadena de nacimiento y muerte a tiempo discreto con espacio de estados en los números enteros.
Además, exploraremos las factorizaciones estocásticas UL y LU de la matriz de probabilidades de transición, así como las transformaciones de Darboux discretas y las matrices espectrales correspondientes.
Soluciones enteras de sistemas lineales de ecuaciones momento diferenciales. Estudio de crecimiento
Alberto Lastra (Universidad de Alcalá)
Friday, September 29th. 14.00 h GMT
Abstract:
En el seminario se motivará la definición de derivada de momentos, como un operador versatil que generaliza la derivada usual, la derivada fraccionaria de Caputo y también la q-derivada en el sentido de Jackson. Se realizará un análisis de las soluciones de sistemas lineales de ecuaciones momento-diferenciales, así como del comportamiento asintótico de sus soluciones en infinito. Este comportamiento se estudiará desde distintos puntos de vista. También se generalizará el concepto de exponencial de una matriz para establecer una solución de manera más compacta.
Estimación con restricciones de forma en regresión funcional usando P-splines
Diego Serrano Ortega (Universidad Carlos III de Madrid)
Friday, July 14th. 14.00 h GMT
Abstract:
La regresión funcional consiste en modelos de regresión que involucran covariables funcionales y/o respuestas funcionales (Ramsay y Silverman, 2005). En muchas ocasiones, el conocimiento previo sobre la naturaleza de la relación entre las covariables y la respuesta (por razones biológicas, médicas, etc.) requiere que los coeficientes funcionales a estimar satisfagan determinadas restricciones de forma, como no negatividad, monotonía o concavidad. Estos requisitos no se satisfacen automáticamente si se usa un método sin restricciones para aproximar el coeficiente funcional. Se propone una combinación de la optimización con técnicas de suavizado, y se compara a través de simulaciones los resultados obtenidos con la literatura existente.
Generalised higher order Freud weights
Kerstin Jordaan (University of South Africa)
Friday, June 30th. 14.00 h GMT
Abstract:
Starting with the work of Géza Freud in the fourth quarter of the 20th century, the study of orthogonal polynomials with respect to exponential weights on the real line has flourished. In this talk I will present some recent results on polynomials orthogonal with respect to Freud-type weights, in particular higher order Freud weights. I will show that the sequence of generalised higher order Freud weights forms a hierarchy of weights, with associated hierarchies for the first moment that can be written as a finite partition sum of generalised hypergeometric functions. The coefficients in the three-term recurrence relation satisfy difference equations which are members of the first discrete Painlev\’e hierarchy that can be used to analyse the asymptotic behaviour of the recurrence coefficients. The asymptotic distribution of the zeros of generalised higher order Freud polynomials orthogonal as $n\to\infty$ follows from the property of regular variation with an appropriate scaling while a mixed recurrence relation satisfied by higher order generalised Freud polynomials is useful in studying other properties of the zeros.
Collaborators: Peter Clarkson and Ana Loureiro (University of Kent, UK).
Buenas, malas y feas bases de polinomios ortogonales en el disco
Leonardo Figueroa (Universidad de Concepción)
Friday, May 19th. 14.00 h GMT
Abstract:
Las bases de polinomios ortogonales en varias variables suelen no ser únicas. En el caso particular del disco unitario ponderado con un peso de tipo Gegenbauer (1-x²-y²)ᵃ, a -1, existe la maravillosa base de F. Zernike (también considerada por R.L. Shapiro, T. Koornwinder y A. Wünsche, entre otros) que, entre otras ventajas, permite codificar operadores diferenciales en forma extremadamente rala (‘sparse’), con las consiguientes ventajas analíticas y computacionales. Si se multiplica un peso de tipo Gegenbauer por factores singulares de la forma |x|ᵇ |y|ᶜ con b,c -1, se obtiene una interesante estructura ortogonal que interactúa naturalmente con operadores construidos en base a las llamadas derivadas de Dunkl y que goza de una íntima conexión con
estructuras ortogonales importantes sobre el triángulo. En esta charla discuto sobre la (no-) existencia de bases de polinomios ortogonales respecto a pesos de Gegenbauer así generalizados que codifiquen operadores ahora Dunkl-diferenciales en forma similarmente rala. Este es trabajo conjunto con Gonzalo Benavides.
Generalized Bernoulli-Barnes polynomials
Yamilet Quintana (Universidad Carlos III de Madrid)
Friday, March 24th. 17.00 h GMT
Abstract:
The main purpose of this talk is to introduce a generalization of the Bernoulli-Barnes polynomials. This generalization comes from suitable modifications of the Mittag-Leffler type function linked to the generating function corresponding to the Bernoulli-Barnes polynomials. We provide several algebraic and combinatorial properties for this new class of polynomials involving the generalized Bernoulli polynomials, Frobenius-Euler functions and Stirling numbers of second kind. Also, we deduce some connection formulae between a subclass of generalized Apostol-type Bernoulli-Barnes polynomials several special polynomials, like Jacobi polynomials, generalized Bernoulli polynomials and Apostol-Euler polynomials. This talk is partially based on joint work with J. L. Ramírez (Universidad Nacional de Colombia) and V. Sirvent (Universidad Católica del Norte, Chile).
New analytic expansions of integral transforms in terms
of elementary functions: Application to special functions
Ester Pérez Sinusía (Universidad de Zaragoza)
Friday, February 24th. 17.00 h GMT
Abstract:
Special functions play an important role in mathematics and physics, as well as in other branches of science such as engineering, chemistry, statistics or economics. Simpler representations of such functions are of great interest from both an analytical and numerical point of view. On the other hand, many special functions admit a representation in terms of integral transforms. In this work, we face the problem of designing a general theory of uniform convergent expansions of integral transforms in terms of elementary functions valid in a large region of the complex plane that include small and large values of a selected variable. This theory is applied to obtain new analytic approximations of different special functions. The new expansions are compared with other known representations to show their advantages and drawbacks.
2023
Multi-applications of multi-orthogonality
Andrei Martínez-Finkelshtein (Baylor University and Universidad de Almería)
Friday, December 9th. 16.30 h GMT
Abstract:
Orthogonal polynomials (OP) belong in a toolbox of any branch of modern science. They appear in multiple applications in engineering, physics, computer science and mathematics. One of the secrets of their ubiquity is that they are on the crossroads of several mathematical branches: analysis, approximation theory, spectral theory, special functions, combinatorics, mathematical physics, numerical analysis, to mention a few. OP have also stimulated the development of new tools and approaches to their study. Their cousins, multiple orthogonal polynomials (MOP), defined by a combination of several orthogonality conditions, are much less known. Their origins can be traced back to the works of Hermite in number theory. However, a general theory of MOP started to develop basically less than 40 years ago. As it often happens, this was simultaneous to appearance of new applications, which brought up new challenges requiring new tools, some of them borrowed from other branches of analysis. In this talk I will try to illustrate some parallels and some striking differences between OP and MOP, as well as to mention some possible emerging applications of MOP.
Orthogonal polynomials in two variables and Quasi-birth and death processes
Lidia Fernández (Universidad de Granada)
Friday, November 25th. 15.00 h GMT
Abstract:
Birth and death processes have many applications and are very useful in modeling. We study some models of quasi-birth and death (QBD) processes arising from the theory of bivariate orthogonal polynomials. We will see how to perform the spectral analysis in the general setting as well as some results about recurrence and the invariant measure of these processes. Afterwards, applications to several examples of bivariate orthogonal polynomials will be presented. We will focus on linear combinations of the Jacobi matrices generated by these polynomials and produce families of either continuous or discrete-time QBD processes. Finally, we show some urn models associated with these QBD processes.
This is a joint work with Manuel Domínguez de la Iglesia.
Symmetric and nonsymmetric representations for Poisson kernels of Askey-Wilson polynomials
Howard Cohl (National Institute of Standards and Technology)
Friday, October 28th. 14.00 h GMT
Abstract:
We discuss the literature on symmetric and nonsymmetric representations for Poisson kernels of Askey-Wilson polynomials. This goes back to the works of Rahman, Verma, Askey, Gasper, Suslov during the 80s and 90s. The symmetric Poisson kernel for Askey-Wilson polynomials was treated in a series of papers by Rahman, Verma and Suslov, and Askey, Rahman and Suslov treated a special form of the nonsymmetric Poisson kernel for Askey-Wilson polynomials in 1996. Even though in all these papers, the analysis was correct, unfortunately, this and all previous symmetric and nonsymmetric Poisson kernels contained typographical errors. We have corrected all symmetric and nonsymmetric representations for these Poisson kernels and as well have computed a new representation of the Askey-Rahman-Suslov nonsymmetric Poisson kernel for Askey-Wilson polynomials using the method of integral representations treated in a recent paper by Cohl and Costas-Santos. We will discuss the form of these representations and as well discuss generating function and arbitrary argument transformation formulas which arise by taking special values of the symmetric representations of these nonsymmetric Poisson kernels. We will also discuss future versions of these results through extension of parameter nonsymmetry.
Spectral Analysis Beyond Random Walks
Ana Foulquié Moreno (Universidade de Aveiro)
Friday, September 30th. 14.00 h GMT
Abstract:
It is known the connection of Random Walks and orthogonal polynomials through Karlin and McGregor spectral analysis This connection can be extended to a more gerenal setting, Markov chains beyond birth and death and multiple orthogonal polynomials. We will present recent results in this direction. This is a joint work with Amílcar Branquinho and Manuel Mañas.
Iterations of Geronimus and Christoffel transformations
Maxim Derevyagin (University of Connecticut)
Friday, June 24th. 14.00 h GMT
Abstract:
Two fundamental discrete Darboux transformations in the theory of orthogonal polynomials are called Geronimus and Christoffel transformations. In this talk, we are going to review the basics of discrete Darboux transformations for orthogonal polynomials. Then, we will discuss the conditions under which one can iterate these transformations and we will present some invariant and semi-invariant properties. In particular, we’ll show what happens to the spectrum of the underlying Jacobi matrices. In addition, we will demonstrate how Geronimus transformations can lead to R_{II}-recurrence relations, which in turn are related to pencils of Jacobi matrices.
Discrete orthogonality of the Askey-Wilson polynomials and other families in the q-Askey scheme
Luis Verde-Star (Universidad Autónoma Metropolitana)
Friday, May 27th. 15.00 h GMT
Abstract:
For some families of basic hypergeometric orthogonal polynomials, that include the Askey-Wilson family, we construct a discrete weight function w defined on a sequence of distinct nodes x_k such that
\tau(p(t))= \sum_{k=0}^\infty p(x_k) w(x_k),
for any polynomial p(t), where \tau is the quasi-definite moment functional that corresponds to an orthogonal polynomial sequence u_n(t) in the q-Askey scheme.
The nodes x_k=b_0+b_1 q^k + b_2 q^{-k}, with at least one of b_1 and b_2 nonzero, determine the sequence v_k(t) of Newton polynomials. Let m_k=\tau(v_k(t)) be the generalized moments of \tau with respect to the Newton sequence. We find the weights w(x_k) by solving the system of equations
m_k=\tau(v_k(t))=\sum_{j=0}^\infty v_k(x_j) w(x_j), \ge 0,
using the inverse of the infinite matrix [v_k(x_j)].
For the most general family in the q-Askey scheme the weights are of the form
w(x_j)=K_j\ \ \hbox{}_3\phi_2(q^j y_1,q^j y_2, q^j y_3;q^j r, q^{2j} s;q;q),
where y_1,y_2,r,s are parameters, y_3={r s}/q y_1 y_2 and
K_j = (-1)^j q^{j(j-1)/2} \frac{(y_1;q)_j (y_2;q)_j (y_3;q)_j }{(q;q)_j (r;q)_j (q^{j-1}s ;q)_j}.
For the Askey-Wilson polynomials with parameters a,b,c,d we obtain y_1=ab, y_2=ac, y_3=ad, r=abcd, s=q a^2.
Transformation and Orthogonal Polynomials
Primitivo B. Acosta-Humánez (Instituto de Matemática UASD)
Friday, April 29th. 15.00 h GMT
Abstract:
In this talk some relations between Darboux Transformation and orthogonal polynomials will be presented. I start setting preliminaries of the classical Darboux transformation for general second order linear differential equations in the form y»+p(x)y’+(mr(x)-q_1(x))y=0, which is transformed into u»+p(x)u’+(mr(x)-q_2(x))u=0. I provide some examples of Darboux transformations for classical orthogonal polynomials. In [1] some algebraic aspects related with orthogonal polynomials were shown. Recently, Darboux transformation was generalized to tensor products of SL_2(C) and orthogonal differential systems.
References:
[1.] Acosta-Humánez, P. B., Morales-Ruiz, J. J., & Weil, J. A. (2011). Galoisian approach to integrability of Schrödinger equation. Reports on Mathematical Physics, 67(3), 305-374.
[2]. Acosta-Humanez, P., Barkatou, M., Sánchez-Cauce, R., & Weil, J. A. (2021). Darboux Transformations for orthogonal differential systems and differential Galois Theory. arXiv preprint arXiv:2101.07470.
Discrete orthogonality of the Askey-Wilson polynomials and other families in the q-Askey scheme
Luis Verde-Star (Universidad Autónoma Metropolitana)
Friday, May 27th. 15.00 h GMT
Abstract:
For some families of basic hypergeometric orthogonal polynomials, that include the Askey-Wilson family, we construct a discrete weight function w defined on a sequence of distinct nodes x_k such that
\tau(p(t))= \sum_{k=0}^\infty p(x_k) w(x_k),
for any polynomial p(t), where \tau is the quasi-definite moment functional that corresponds to an orthogonal polynomial sequence u_n(t) in the $q$-Askey scheme.
The nodes x_k=b_0+b_1 q^k + b_2 q^{-k}, with at least one of b_1 and b_2 nonzero, determine the sequence v_k(t) of Newton polynomials. Let m_k=\tau(v_k(t)) be the generalized moments of \tau with respect to the Newton sequence. We find the weights w(x_k) by solving the system of equations
m_k=\tau(v_k(t))=\sum_{j=0}^\infty v_k(x_j) w(x_j), k \ge 0,
using the inverse of the infinite matrix [v_k(x_j)].
For the most general family in the $q$-Askey scheme the weights are of the form
$$w(x_j)=K_j\ \ \hbox{}_3\phi_2(q^j y_1,q^j y_2, q^j y_3;q^j r, q^{2j} s;q;q),$$
where $ y_1,y_2,r,s$ are parameters, $y_3={r s}/q y_1 y_2$ and
$$K_j = (-1)^j q^{j(j-1)/2} \frac{(y_1;q)_j (y_2;q)_j (y_3;q)_j }{(q;q)_j (r;q)_j (q^{j-1}s ;q)_j}.$$
For the Askey-Wilson polynomials with parameters $a,b,c,d$ we obtain
$y_1=ab,\ \ y_2=ac,\ \ y_3=ad,\ \ r=abcd,\ \ s=q a^2.$
On symmetric semi-classical orthogonal polynomials and some of their extensions
Maria das Neves Rebocho (Universidade da Beira Interior)
Friday, March 18th. 15.00 h GMT
Abstract:
This talk concerns the so-called direct problem for orthogonal polynomials. We take the sequences of orthogonal polynomials whose Stieltjes function, S, satisfies a Riccati type differential equation with polynomial coefficients,
AS’=BS2+CS+D, A\neq 0,
and we seek formulae for the three-term recurrence relation coefficients of the orthogonal polynomials, given A, B, C, D.
The symmetric case under the restriction max{deg(C) – 1, max{deg(A), deg(B)} – 2}=2 will be described in detail: we deduce non-linear difference equations for the recurrence relation coefficients, some of them identified as discrete Painlevé equations.
Techniques to investigate the existence of periodic solutions in control systems
Baltazar Aguirre Hernández (Universidad Autónoma Metropolitana – Iztapalapa)
Friday, February 18th. 15.00 h GMT
Abstract: Techniques to investigate the existence of periodic solutions in control systemsAbstract: The problem of investigating the existence of periodic solutions is considered a very difficult problem. In this conference we will focus on a type of control systems and we will explain 3 techniques to investigate the existence of periodic solutions: in one technique an infinite system of nonlinear equations has to be solved, in another technique a fixed point problem has to be solved and the third would be an approximate technique to detect the periodic solutions by means of a finite Fourier series.
2022
On a family of Jacobi type polynomials as eigenfunctions of 2×2 hypergeometric operators
Mirta Castro Smirnova (Universidad de Sevilla)
Friday, December 10th. 15.00 h GMT
Abstract: In the last few years, the search for examples of matrix-valued orthogonal polynomials that are common eigenfunctions of a second order differential operator has received a lot of attention after the seminal work of A. Durán in the nineties.
Recently, a new family of orthogonal polynomials of size 2×2 was introduced by C. Calderón et al. ( J. of Approx Theory, 2018), which are common eigenfunctions of a differential operator of hipergeometric type (in the sense defined by A. Tirao, Proc. Nac. Acad. Sci, 2003), with diagonal matrix eigenvalues. We give some structural formulas for this family of matrix-valued orthogonal polynomials.
This is a joint work with Celeste Calderón from Universidad Nacional de Cuyo, Mendoza, Argentina.
Semiclassical orthogonal polynomials and nonlinear differential equations
Galina Filipuk (Warsaw University)
Friday, November 26th. 15.00 h GMT
Abstract: In this talk I shall explain how the study of nonlinear differential equations can shed some light on the theory of semiclassical orthogonal polynomials and vice versa.
Recurrence relations for moment sequences of discrete semiclassical orthogonal polynomials
Diego Dominici (Johannes Kepler University)
Friday, October 29th. 14.00 h GMT
Abstract: In this talk, we will present some results about the moments (in different bases) of discrete semiclassical orthogonal polynomials. Our approach is formulated in terms of differential equations and differential operators characterizing different families. We give examples for (most of) the polynomials of class less or equal than 2.
On certain system of symmetric Al-Salam–Carlitz I-Sobolev type orthogonal polynomials of higher order
Carlos Hermoso (Universidad de Alcalá)
Friday, October 1st. 14.00 h GMT
Abstract: We analyze a polynomial sequence associated to a Sobolev-type inner product, which involves an arbitrary number (j) of q-derivatives on the two boundaries of the corresponding orthogonality interval, and that is closely related to the well known family of Al-Salam–Carlitz I orthogonal polynomials.
We present several interesting results, namely: connection formulas, ladder operators, and two versions of the holonomic second order q-difference equations satisfied by the aforementioned nonstandard sequence.
This is a joint work with Edmundo Huertas, Alberto Lastra and Anier Soria-Lorente.
Generalised higher order Freud weights
Kerstin Jordaan (University of South Africa)
Friday, June 30th. 14.00 h GMT
Abstract:
Las bases de polinomios ortogonales en varias variables suelen no ser
únicas. En el caso particular del disco unitario ponderado con un peso
de tipo Gegenbauer (1-x²-y²)ᵃ, a > -1, existe la maravillosa base de
F. Zernike (también considerada por R.L. Shapiro, T. Koornwinder y A.
Wünsche, entre otros) que, entre otras ventajas, permite codificar
operadores diferenciales en forma extremadamente rala (‘sparse’), con
las consiguientes ventajas analíticas y computacionales.
Si se multiplica un peso de tipo Gegenbauer por factores singulares de
la forma |x|ᵇ |y|ᶜ con b,c > -1, se obtiene una interesante estructura
ortogonal que interactúa naturalmente con operadores construidos en
base a las llamadas derivadas de Dunkl y que goza de una íntima
conexión con estructuras ortogonales importantes sobre el triángulo.
En esta charla discuto sobre la (no-) existencia de bases de
polinomios ortogonales respecto a pesos de Gegenbauer así
generalizados que codifiquen operadores ahora Dunkl-diferenciales en
forma similarmente rala.
Este es trabajo conjunto con Gonzalo Benavides.
Generalized Bernoulli-Barnes polynomials
Yamilet Quintana (Universidad Carlos III de Madrid)
Friday, March 24th. 17.00 h GMT
Abstract:
The main purpose of this talk is to introduce a generalization of the Bernoulli-Barnes polynomials. This generalization comes from suitable modifications of the Mittag-Leffler type function linked to the generating function corresponding to the Bernoulli-Barnes polynomials. We provide several algebraic and combinatorial properties for this new class of polynomials involving the generalized Bernoulli polynomials, Frobenius-Euler functions and Stirling numbers of second kind. Also, we deduce some connection formulae between a subclass of generalized Apostol-type Bernoulli-Barnes polynomials several special polynomials, like Jacobi polynomials, generalized Bernoulli polynomials and Apostol-Euler polynomials. This talk is partially based on joint work with J. L. Ramírez (Universidad Nacional de Colombia) and V. Sirvent (Universidad Católica del Norte, Chile).
New analytic expansions of integral transforms in terms
of elementary functions: Application to special functions
Ester Pérez Sinusía (Universidad de Zaragoza)
Friday, February 24th. 17.00 h GMT
Abstract:
Special functions play an important role in mathematics and physics, as well as in other branches of science such as engineering, chemistry, statistics or economics. Simpler representations of such functions are of great interest from both an analytical and numerical point of view. On the other hand, many special functions admit a representation in terms of integral transforms. In this work, we face the problem of designing a general theory of uniform convergent expansions of integral transforms in terms of elementary functions valid in a large region of the complex plane that include small and large values of a selected variable. This theory is applied to obtain new analytic approximations of different special functions. The new expansions are compared with other known representations to show their advantages and drawbacks.
2021
Multi-applications of multi-orthogonality
Andrei Martínez-Finkelshtein (Baylor University and Universidad de Almería)
Friday, December 9th. 16.30 h GMT
Abstract:
Orthogonal polynomials (OP) belong in a toolbox of any branch of modern science. They appear in multiple applications in engineering, physics, computer science and mathematics. One of the secrets of their ubiquity is that they are on the crossroads of several mathematical branches: analysis, approximation theory, spectral theory, special functions, combinatorics, mathematical physics, numerical analysis, to mention a few. OP have also stimulated the development of new tools and approaches to their study. Their cousins, multiple orthogonal polynomials (MOP), defined by a combination of several orthogonality conditions, are much less known. Their origins can be traced back to the works of Hermite in number theory. However, a general theory of MOP started to develop basically less than 40 years ago. As it often happens, this was simultaneous to appearance of new applications, which brought up new challenges requiring new tools, some of them borrowed from other branches of analysis. In this talk I will try to illustrate some parallels and some striking differences between OP and MOP, as well as to mention some possible emerging applications of MOP.
Orthogonal polynomials in two variables and Quasi-birth and death processes
Lidia Fernández (Universidad de Granada)
Friday, November 25th. 15.00 h GMT
Abstract:
Birth and death processes have many applications and are very useful in modeling. We study some models of quasi-birth and death (QBD) processes arising from the theory of bivariate orthogonal polynomials. We will see how to perform the spectral analysis in the general setting as well as some results about recurrence and the invariant measure of these processes. Afterwards, applications to several examples of bivariate orthogonal polynomials will be presented. We will focus on linear combinations of the Jacobi matrices generated by these polynomials and produce families of either continuous or discrete-time QBD processes. Finally, we show some urn models associated with these QBD processes.
This is a joint work with Manuel Domínguez de la Iglesia.
Symmetric and nonsymmetric representations for Poisson kernels of Askey-Wilson polynomials
Howard Cohl (National Institute of Standards and Technology)
Friday, October 28th. 14.00 h GMT
Abstract:
We discuss the literature on symmetric and nonsymmetric representations for Poisson kernels of Askey-Wilson polynomials. This goes back to the works of Rahman, Verma, Askey, Gasper, Suslov during the 80s and 90s. The symmetric Poisson kernel for Askey-Wilson polynomials was treated in a series of papers by Rahman, Verma and Suslov, and Askey, Rahman and Suslov treated a special form of the nonsymmetric Poisson kernel for Askey-Wilson polynomials in 1996. Even though in all these papers, the analysis was correct, unfortunately, this and all previous symmetric and nonsymmetric Poisson kernels contained typographical errors. We have corrected all symmetric and nonsymmetric representations for these Poisson kernels and as well have computed a new representation of the Askey-Rahman-Suslov nonsymmetric Poisson kernel for Askey-Wilson polynomials using the method of integral representations treated in a recent paper by Cohl and Costas-Santos. We will discuss the form of these representations and as well discuss generating function and arbitrary argument transformation formulas which arise by taking special values of the symmetric representations of these nonsymmetric Poisson kernels. We will also discuss future versions of these results through extension of parameter nonsymmetry.
Spectral Analysis Beyond Random Walks
Ana Foulquié Moreno (Universidade de Aveiro)
Friday, September 30th. 14.00 h GMT
Abstract:
It is known the connection of Random Walks and orthogonal polynomials through Karlin and McGregor spectral analysis This connection can be extended to a more gerenal setting, Markov chains beyond birth and death and multiple orthogonal polynomials. We will present recent results in this direction. This is a joint work with Amílcar Branquinho and Manuel Mañas.
Iterations of Geronimus and Christoffel transformations
Maxim Derevyagin (University of Connecticut)
Friday, June 24th. 14.00 h GMT
Abstract:
Two fundamental discrete Darboux transformations in the theory of orthogonal polynomials are called Geronimus and Christoffel transformations. In this talk, we are going to review the basics of discrete Darboux transformations for orthogonal polynomials. Then, we will discuss the conditions under which one can iterate these transformations and we will present some invariant and semi-invariant properties. In particular, we’ll show what happens to the spectrum of the underlying Jacobi matrices. In addition, we will demonstrate how Geronimus transformations can lead to R_{II}-recurrence relations, which in turn are related to pencils of Jacobi matrices.
Discrete orthogonality of the Askey-Wilson polynomials and other families in the q-Askey scheme
Luis Verde-Star (Universidad Autónoma Metropolitana)
Friday, May 27th. 15.00 h GMT
Abstract:
For some families of basic hypergeometric orthogonal polynomials, that include the Askey-Wilson family, we construct a discrete weight function w defined on a sequence of distinct nodes x_k such that
\tau(p(t))= \sum_{k=0}^\infty p(x_k) w(x_k),
for any polynomial p(t), where \tau is the quasi-definite moment functional that corresponds to an orthogonal polynomial sequence u_n(t) in the q-Askey scheme.
The nodes x_k=b_0+b_1 q^k + b_2 q^{-k}, with at least one of b_1 and b_2 nonzero, determine the sequence v_k(t) of Newton polynomials. Let m_k=\tau(v_k(t)) be the generalized moments of \tau with respect to the Newton sequence. We find the weights w(x_k) by solving the system of equations
m_k=\tau(v_k(t))=\sum_{j=0}^\infty v_k(x_j) w(x_j), \ge 0,
using the inverse of the infinite matrix [v_k(x_j)].
For the most general family in the q-Askey scheme the weights are of the form
w(x_j)=K_j\ \ \hbox{}_3\phi_2(q^j y_1,q^j y_2, q^j y_3;q^j r, q^{2j} s;q;q),
where y_1,y_2,r,s are parameters, y_3={r s}/q y_1 y_2 and
K_j = (-1)^j q^{j(j-1)/2} \frac{(y_1;q)_j (y_2;q)_j (y_3;q)_j }{(q;q)_j (r;q)_j (q^{j-1}s ;q)_j}.
For the Askey-Wilson polynomials with parameters a,b,c,d we obtain y_1=ab, y_2=ac, y_3=ad, r=abcd, s=q a^2.
Transformation and Orthogonal Polynomials
Primitivo B. Acosta-Humánez (Instituto de Matemática UASD)
Friday, April 29th. 15.00 h GMT
Abstract:
In this talk some relations between Darboux Transformation and orthogonal polynomials will be presented. I start setting preliminaries of the classical Darboux transformation for general second order linear differential equations in the form y»+p(x)y’+(mr(x)-q_1(x))y=0, which is transformed into u»+p(x)u’+(mr(x)-q_2(x))u=0. I provide some examples of Darboux transformations for classical orthogonal polynomials. In [1] some algebraic aspects related with orthogonal polynomials were shown. Recently, Darboux transformation was generalized to tensor products of SL_2(C) and orthogonal differential systems.
References:
[1.] Acosta-Humánez, P. B., Morales-Ruiz, J. J., & Weil, J. A. (2011). Galoisian approach to integrability of Schrödinger equation. Reports on Mathematical Physics, 67(3), 305-374.
[2]. Acosta-Humanez, P., Barkatou, M., Sánchez-Cauce, R., & Weil, J. A. (2021). Darboux Transformations for orthogonal differential systems and differential Galois Theory. arXiv preprint arXiv:2101.07470.
Discrete orthogonality of the Askey-Wilson polynomials and other families in the q-Askey scheme
Luis Verde-Star (Universidad Autónoma Metropolitana)
Friday, May 27th. 15.00 h GMT
Abstract:
For some families of basic hypergeometric orthogonal polynomials, that include the Askey-Wilson family, we construct a discrete weight function w defined on a sequence of distinct nodes x_k such that
\tau(p(t))= \sum_{k=0}^\infty p(x_k) w(x_k),
for any polynomial p(t), where \tau is the quasi-definite moment functional that corresponds to an orthogonal polynomial sequence u_n(t) in the $q$-Askey scheme.
The nodes x_k=b_0+b_1 q^k + b_2 q^{-k}, with at least one of b_1 and b_2 nonzero, determine the sequence v_k(t) of Newton polynomials. Let m_k=\tau(v_k(t)) be the generalized moments of \tau with respect to the Newton sequence. We find the weights w(x_k) by solving the system of equations
m_k=\tau(v_k(t))=\sum_{j=0}^\infty v_k(x_j) w(x_j), k \ge 0,
using the inverse of the infinite matrix [v_k(x_j)].
For the most general family in the $q$-Askey scheme the weights are of the form
$$w(x_j)=K_j\ \ \hbox{}_3\phi_2(q^j y_1,q^j y_2, q^j y_3;q^j r, q^{2j} s;q;q),$$
where $ y_1,y_2,r,s$ are parameters, $y_3={r s}/q y_1 y_2$ and
$$K_j = (-1)^j q^{j(j-1)/2} \frac{(y_1;q)_j (y_2;q)_j (y_3;q)_j }{(q;q)_j (r;q)_j (q^{j-1}s ;q)_j}.$$
For the Askey-Wilson polynomials with parameters $a,b,c,d$ we obtain
$y_1=ab,\ \ y_2=ac,\ \ y_3=ad,\ \ r=abcd,\ \ s=q a^2.$
On symmetric semi-classical orthogonal polynomials and some of their extensions
Maria das Neves Rebocho (Universidade da Beira Interior)
Friday, March 18th. 15.00 h GMT
Abstract:
This talk concerns the so-called direct problem for orthogonal polynomials. We take the sequences of orthogonal polynomials whose Stieltjes function, S, satisfies a Riccati type differential equation with polynomial coefficients,
AS’=BS2+CS+D, A\neq 0,
and we seek formulae for the three-term recurrence relation coefficients of the orthogonal polynomials, given A, B, C, D.
The symmetric case under the restriction max{deg(C) – 1, max{deg(A), deg(B)} – 2}=2 will be described in detail: we deduce non-linear difference equations for the recurrence relation coefficients, some of them identified as discrete Painlevé equations.
Techniques to investigate the existence of periodic solutions in control systems
Baltazar Aguirre Hernández (Universidad Autónoma Metropolitana – Iztapalapa)
Friday, February 18th. 15.00 h GMT
Abstract: Techniques to investigate the existence of periodic solutions in control systemsAbstract: The problem of investigating the existence of periodic solutions is considered a very difficult problem. In this conference we will focus on a type of control systems and we will explain 3 techniques to investigate the existence of periodic solutions: in one technique an infinite system of nonlinear equations has to be solved, in another technique a fixed point problem has to be solved and the third would be an approximate technique to detect the periodic solutions by means of a finite Fourier series.
2020
On a family of Jacobi type polynomials as eigenfunctions of 2×2 hypergeometric operators
Mirta Castro Smirnova (Universidad de Sevilla)
Friday, December 10th. 15.00 h GMT
Abstract: In the last few years, the search for examples of matrix-valued orthogonal polynomials that are common eigenfunctions of a second order differential operator has received a lot of attention after the seminal work of A. Durán in the nineties.
Recently, a new family of orthogonal polynomials of size 2×2 was introduced by C. Calderón et al. ( J. of Approx Theory, 2018), which are common eigenfunctions of a differential operator of hipergeometric type (in the sense defined by A. Tirao, Proc. Nac. Acad. Sci, 2003), with diagonal matrix eigenvalues. We give some structural formulas for this family of matrix-valued orthogonal polynomials.
This is a joint work with Celeste Calderón from Universidad Nacional de Cuyo, Mendoza, Argentina.
Semiclassical orthogonal polynomials and nonlinear differential equations
Galina Filipuk (Warsaw University)
Friday, November 26th. 15.00 h GMT
Abstract: In this talk I shall explain how the study of nonlinear differential equations can shed some light on the theory of semiclassical orthogonal polynomials and vice versa.
Recurrence relations for moment sequences of discrete semiclassical orthogonal polynomials
Diego Dominici (Johannes Kepler University)
Friday, October 29th. 14.00 h GMT
Abstract: In this talk, we will present some results about the moments (in different bases) of discrete semiclassical orthogonal polynomials. Our approach is formulated in terms of differential equations and differential operators characterizing different families. We give examples for (most of) the polynomials of class less or equal than 2.
On certain system of symmetric Al-Salam–Carlitz I-Sobolev type orthogonal polynomials of higher order
Carlos Hermoso (Universidad de Alcalá)
Friday, October 1st. 14.00 h GMT
Abstract: We analyze a polynomial sequence associated to a Sobolev-type inner product, which involves an arbitrary number (j) of q-derivatives on the two boundaries of the corresponding orthogonality interval, and that is closely related to the well known family of Al-Salam–Carlitz I orthogonal polynomials.
We present several interesting results, namely: connection formulas, ladder operators, and two versions of the holonomic second order q-difference equations satisfied by the aforementioned nonstandard sequence.
This is a joint work with Edmundo Huertas, Alberto Lastra and Anier Soria-Lorente.
